개발자라면 한번쯤은 보러오는 곳
[Computer Vision] Regression 본문
Linear Functions

- 파라메타(베타)를 전치시키고 곱해주면 함수의 꼴로 표현 할 수 있다. 이러한 파라메타를 찾는것이 목표
- 입력값 x는 한개만 존재하는 것이 아닌 R^d 즉 d는 차원으로써 3차원 4차원 등등 여러개의 값을 가질 수 있다. 이를 벡터로 표현할 수 있다.

- 즉 가장 찾아야하는 원본 y와 비슷한 함수를 찾는 것이 목표이다. 이를 위해서는 파라메타(베타)를 가장 최적에 가깝도록 만들어야 한다.

Loss-Function or Cost-Function(손실함수)
MSE(Mean squared error)

- 오차의 제곱값을 평균을 만든다. 이를 통해서 모델이 얼마나 잘 들어맞는지 평가 가능

손실 최소 함수

Intuition on Minimizing MSE Loss = MSE 손실 최소화에 대한 직관

베타 = 1 이기때문에 손실함수가 0이 되어 완벽하다고 할 수 있다.


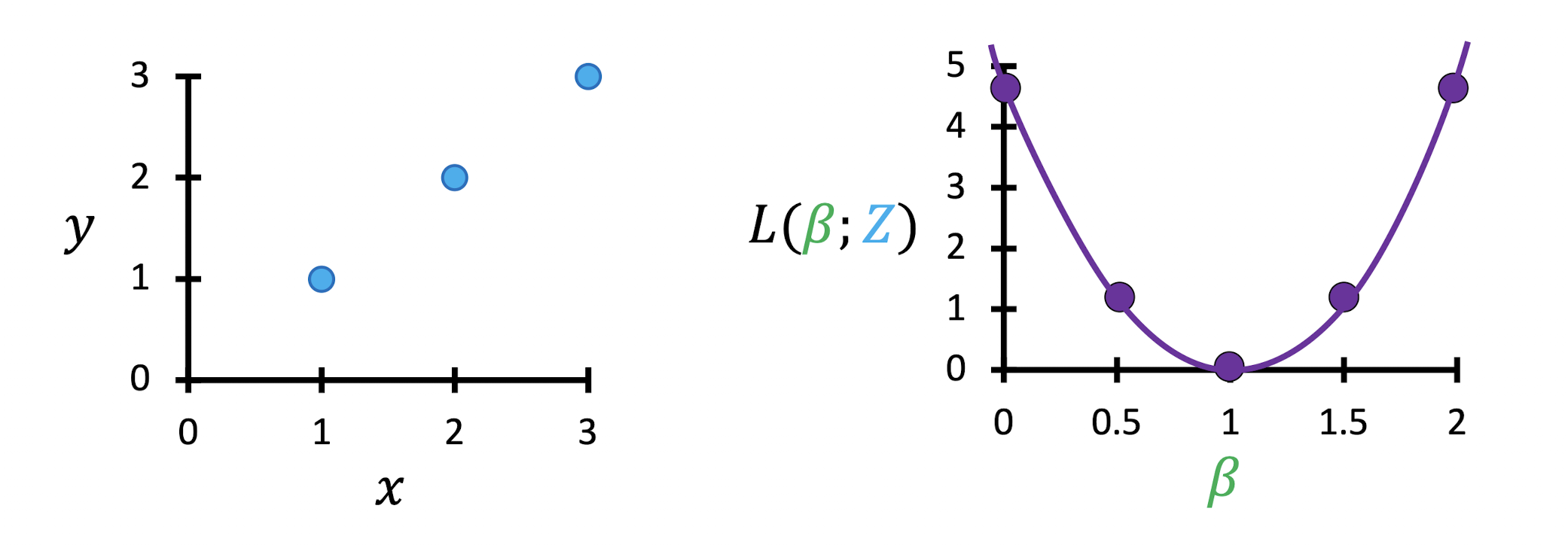
손실함수는 2차원의 함수형태를 가질 것이다.
손실함수를 미분하여 극소값의 지점을 찾으면 된다.
하지만 현실에서의 데이터는 깔끔하지 않고, 모든 loss를 계산하기 때문에 비효율적이다.
Quadratic Funcion


위와 같은 데이터들의 분포가 있다는 가정하에, 1차함수로써 이 데이터를 표현하면 어떻게 될까? 아무리 기울기를 바꾸어보아도 곡선의 모양에 최적화 시킬 수 없을 것이다. 즉 1차원으로써는 최적의 값을 찾을 수 없다는 뜻이다. 그렇다고 non-linear model을 설정하면 해결 될 것 같지만, 앞서 배웠듯 non-linear은 처리하기 까다롭다. 그래서 feature map라는 개념이 등장한다.

feature map을 적용한 알고리즘의 순서이다.

Why not throw in lots of features? = 왜 많은 features를 사용하지 않을까?
- 차원이 커지면 모델의 자유도가 높아져 표현범위가 넓어진다. -> 오버피팅


- 낮은 차원의 모델이 new data에 대해 오차값이 적다.
Higher capacity -> more likely to overfit (model family has high variance)
-> High variance : Increase data size n(i.e. gather more labeled data)(모델 데이터를 줄려서 해결/but 질 좋은 데이터가 있다면 극복 가능)
Lower capacity -> more likely to underfit (model family has high bias)
-> High bias : Increase model capacity d(모델 데이터를 더 늘려서 해결)
'학교 수업 > Computer Vision' 카테고리의 다른 글
| [Computer Vision] Classification (0) | 2022.10.27 |
|---|---|
| [Computer Vision] Gradient Descent (0) | 2022.10.22 |
| [Computer Vision] Machine Learning (1) | 2022.10.15 |
| [Computer Vision] Edge detection (0) | 2022.10.12 |
| [Computer Vision] Filters (1) | 2022.10.08 |




